Aussagenkalkül

Als Aussagenkalkül bezeichnet man ein formales System zur Beschreibung der Aussagenlogik (siehe oben). Strenggenommen sind zwei Kalküle schon dann verschieden, wenn sie unterschiedliche Grundbausteine benutzen. In diesem Sinne gibt es verschiedene Aussagenkalküle, die die klassische zweiwertige Aussagenlogik beschreiben. Da die Tautologien in allen diesen Kalkülen übereinstimmen, ist es gerechtfertigt, die Kalküle als äquivalent anzusehen und von dem Aussagenkalkül der zweiwertigen Aussagenlogik zu sprechen (auf andere Aussagenkalküle wird hier nicht eingegangen).

Der Aussagenkalkül besteht aus folgenden Grundzeichen:

1. Aussagenvariablen: p₁, p₂, p₃, . . . ,
2. Funktoren oder Konnektoren:
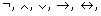
3. technische Zeichen: (, ).

Aus diesen Grundzeichen (Alphabet) entstehen durch Aneinanderreihung (endliche) Zeichenreihen. Induktiv werden aus der Menge der Zeichenreihen die Ausdrücke oder Formeln durch folgende Vorschrift ausgesondert:

1. Alle Aussagenvariablen sind Ausdrücke (die nicht weiter zerlegbar sind und daher atomar oder Atomausdruck genannt werden).
2. Sind 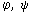Ausdrücke, dann sind auch 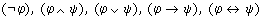Ausdrücke.
3. Keine weiteren Zeichenreihen sind Ausdrücke.

Um unnötige Klammern einzusparen, vereinbart man: Außenklammern dürfen weggelassen werden, bindet stärker als alle anderen Konnektoren, und binden stärker als und . Für schreibt man kürzer . Die korrekte Bildung von Ausdrücken gehört zur Grundlage des Aussagenkalküls.

Die Semantik befasst sich mit dem „Wahrheitsbegriff“, der i.allg. unzulänglich präzisiert ist. Zumindest für die Mathematik lässt sich der Wahrheitsbegriff hinlänglich genau festlegen.

Mathematische Aussagen sind in der Regel so präzise formuliert, dass sie entweder wahr oder falsch sind. Dieses Prinzip der Zweiwertigkeit drückt sich dadurch aus, dass Aussagen höchstens diese zwei Wahrheitswerte wahr oder 1 bzw. falsch oder 0 annehmen können. In der Semantik des Aussagenkalküls wird u. a. der Wahrheitswert von zusammengesetzten Ausdrücken bestimmt, wenn der Wahrheitswert für die Teilausdrücke schon bekannt ist. Dies erfolgt wieder induktiv über den Aufbau der Ausdrücke. Dazu sei V die Menge der Aussagenvariablen und F : V {0, 1} eine Abbildung, die jeder Variablen den Wert 0 (falsch) oder 1 (wahr) zuordnet. F heißt Belegung der Aussagenvariablen mit Wahrheitswerten. Für die Menge Ausd aller Ausdrücke wird F induktiv zu F* : Ausd {0, 1} erweitert:

1. Ist j atomar (also eine Aussagenvariable), dann sei F*(j) = F(j).
2. Für zusammengesetzte Ausdrücke erfolgt die Definition entsprechend der Kompliziertheit der Ausdrücke.
   

Auf diese Weise ist bei gegebener Belegung der Wahrheitswert eines aussagenlogischen Ausdrucks stets berechenbar. Ist j ein Ausdruck, der bei jeder Belegung wahr wird, dann ist j aussagenlogisch allgemeingültig oder eine aussagenlogische Tautologie. Man vergleiche hierzu auch die Ausführungen zur Aussagenlogik (siehe oben).

© 2004-2005, Prof. Dr. D. Hannemann, Gelsenkirchen